Our group studies the rheology and the fluid dynamics of viscoelastic suspensions by numerical simulations. Suspensions are materials constituted by solid particles immersed in a liquid matrix. The addition of solid inclusions in Newtonian media give arise to a number of properties that are typical of non-Newtonian fluids. If the suspending liquid shows itself viscoelastic properties, the rheological response is even more complex. In addition, fluid viscoelasticity may lead to unusual particle dynamics, not observed in Newtonian liquids. Particle size and shape, solid concentration and confinement effects strongly affect the bulk rheology and the local microstructure. Our aim is to elucidate the role of fluid elasticity on the bulk response of solid suspensions and to predict the dynamics of the flowing particles. The study is carried out by direct numerical simulations whereby the macroscopic governing equations, with a proper choice for the constitutive model, are solved and the motion of each particle is computed. The hydrodynamic interactions are automatically included in the system of equations and, as such, no model is required. We apply the simulation results to design viscoelasticity-based microfluidic devices to achieve operations that would require complex chips or would not be possible with Newtonian suspending liquids (see Officina Microfluidics).
Manager: Gaetano D’Avino
Members: Massimiliano Villone
Particle rotation
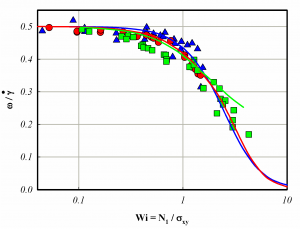
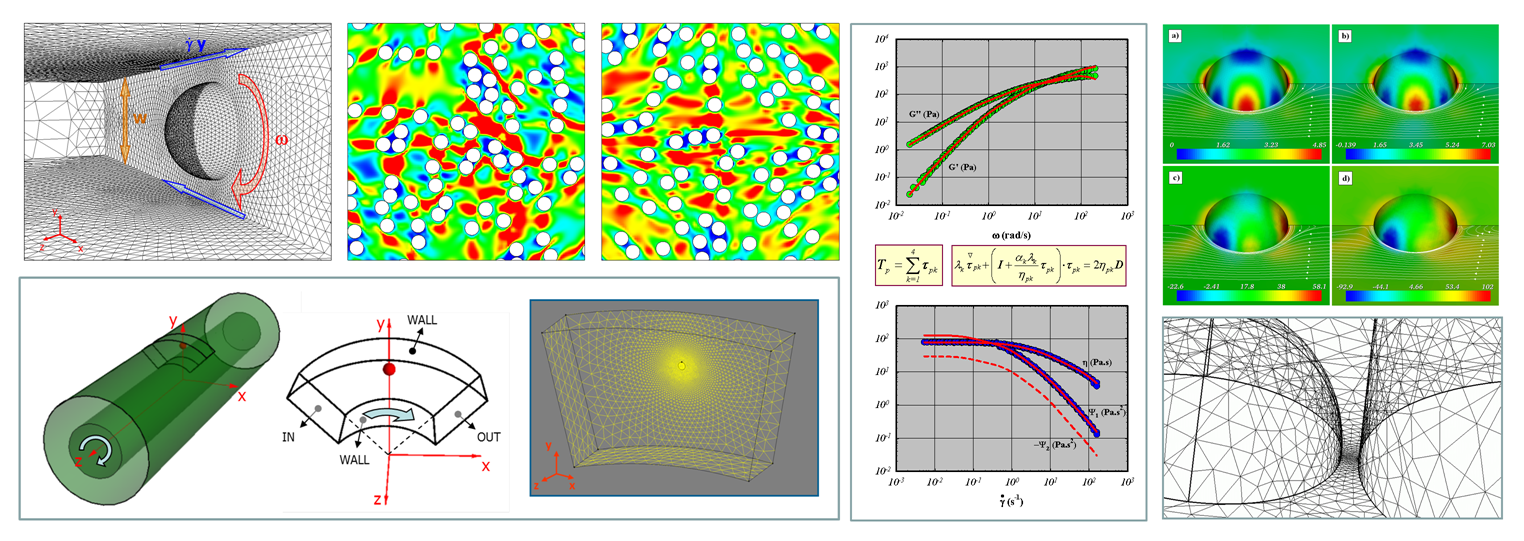
Fig. 1 – Experimental (symbols) and numerical (lines) normalized particle angular velocity as a function of the Weissenberg number for different suspending liquids: wormlike micellar solution (blue), PIB in Pristane (red), Boger fluid (green)
The well-known Einstein’s result states that a single, spherical, non-Brownian, inertialess particle suspended in an inertialess Newtonian fluid under an unbounded shear flow rotates with angular velocity equal to one-half of the applied shear rate. If the suspending fluid is viscoelastic, a slowing down of the rotation rate is found [1, 2]. Interestingly, the particle angular velocity, plotted as a function of the Weissenberg number (defined as the ratio between the first normal stress difference and the shear stress), is independent of the rheological properties of the suspending liquid (see Fig. 1). The quantitative agreement between experiments and simulations (where constitutive equations describing the experimental fluids are used) confirm the existence of a unique master scaling [3]. We extended the study to account for the effect of confinement on the particle rotation rate [4]. As for a Newtonian suspending fluid, the presence of walls further contributes to the slowing down effect.
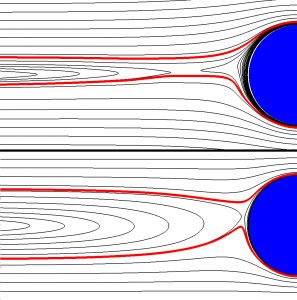
Fig. 2 – Streamlines around a rotating sphere on the flow-gradient plane for an unbounded (top) and a confined (bottom) shear flow at Wi = 2. The suspending fluid is modelled by the Giesekus constitutive equation.
Both fluid viscoelasticity and confinement also affect the streamlines around the rotating particle. For the unbounded case (Fig. 2, top), the viscoelasticity opens up the closed orbits around the sphere observed for an inertialess Newtonian fluid. Three regions can be identified: i) fluid streamlines that approach and pass the particle, ii) attractive closed orbit surrounding the sphere, iii) recirculation regions where the fluid moves towards the particle and changes its direction. The loss of symmetry with respect to the Newtonian case is also evident. The presence of confinement (Fig. 2, bottom) leads to a larger recirculation region whereas the attractive streamline approaches the particle [4].
- D’Avino et al., J. Rheol., 52, 1331-1346 (2008)
- Snijkers et al., J. Rheol., 53, 459-480 (2009)
- Snijkers et al., J. Non-Newtonian Fluid Mech., 166, 363-372 (2011)
- D’Avino et al., J. Non-Newtonian Fluid Mech., 157, 101-107 (2009)
Particle migration

Fig. 1 – Experimental (symbols) and numerical (solid lines) trajectories of a sphere suspended in a wormlike micellar solution in Couette flow
Cross-stream migration, i.e. the motion of particles transversally to the main flow direction, occurs in viscoelastic suspending liquids due to an imbalance of normal stresses around the particle. The migration direction is strongly dependent on the fluid rheology, the confinement ratio and, above all, the flow field. Our 3D numerical simulations show that, in planar shear flow, the viscoelasticity always drives the particle towards the closest wall [1-3]. In such a flow, the normal stress imbalance is caused by confinement effects. In a Couette geometry (see Fig. 1), the coupled effect of the curvature of the velocity profile and the particle-wall hydrodynamic interactions gives arise to an unstable separatrix close to the inner cylinder, thus leading to a bistability dynamics [4].

Fig. 3 – Migration of a sphere in a viscoelastic fluid flowing in a pipe. The initial position is r/R = 0.255, with R the cylinder radius. The colors are the first normal stress difference
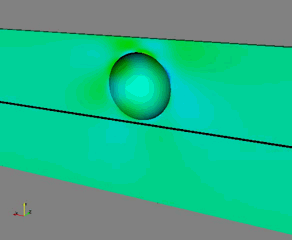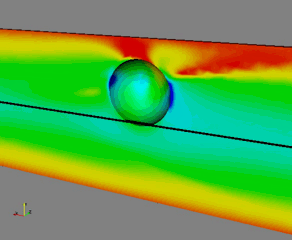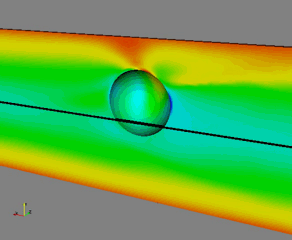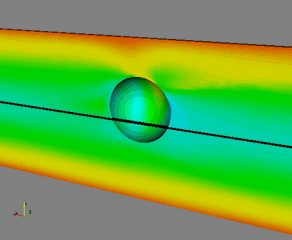
Fig. 2 – Migration of a sphere in a viscoelastic fluid flowing in a pipe. The initial position is r/R = 0.22, with R the cylinder radius. The colors are the first normal stress difference
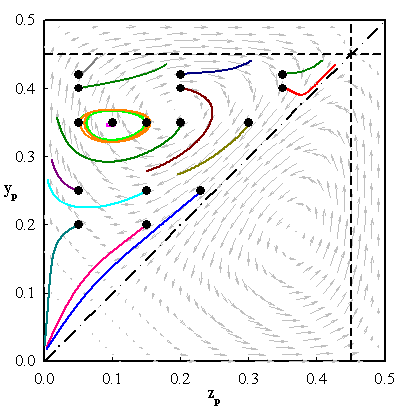
Fig. 4 – Particle migration trajectories for different initial
positions projected on the channel cross-section. The particle is suspended in a Giesekus fluid flowing in a square-shaped channel. The grey arrows are the secondary flows of the fluid without particle. Only the left half of the upper-right
quadrant of the cross-section is reported
A similar scenario occurs for a suspension flowing in a cylinder or in a wide-slit channel [5-6]. In both cases, the particles may migrate towards the channel centerline/centerplane or towards the walls depending on the initial position (inversion of Segrè-Silberberg effect) (see Figs. 2 and 3). Fluid rheology affects the position of the separatrix that moves towards the wall for weaker shear-thinning fluids. The latter opens-up the possibility to achieve 3D particle flow-focusing in a straight pipe (see Officina Microfluidics). A more complex scenario occurs in channels with a square cross-section [7]. The competition between migration and secondary flows leads to the appearance of further equilibrium points between the centerline and the walls (see Fig. 4). Particles driven towards such positions trace out a spiral trajectory, following the vortex structure of the secondary flows. As the particle dimension is increased or the Weissenberg number is reduced, the cross-streamline migration velocity overcomes the secondary flow velocity and the most of the particles are attracted towards the channel centerline.
- D’Avino et al., Comput. Fluids, 39, 709-721 (2010)
- D’Avino et al., J. Non-Newtonian Fluid Mech., 175, 466-474 (2010)
- Caserta et al., Soft Matter, 7, 1100-1106 (2011)
- D’Avino et al., Rheol. Acta, 51, 215–234 (2012)
- Villone et al., Comput. Fluids, 42, 82-91 (2011)
- Villone et al., J. Non-Newtonian Fluid Mech., 166, 1396-1405 (2011)
- Villone et al., J. Non-Newtonian Fluid Mech., 195, 1-8 (2013)
Particle chaining
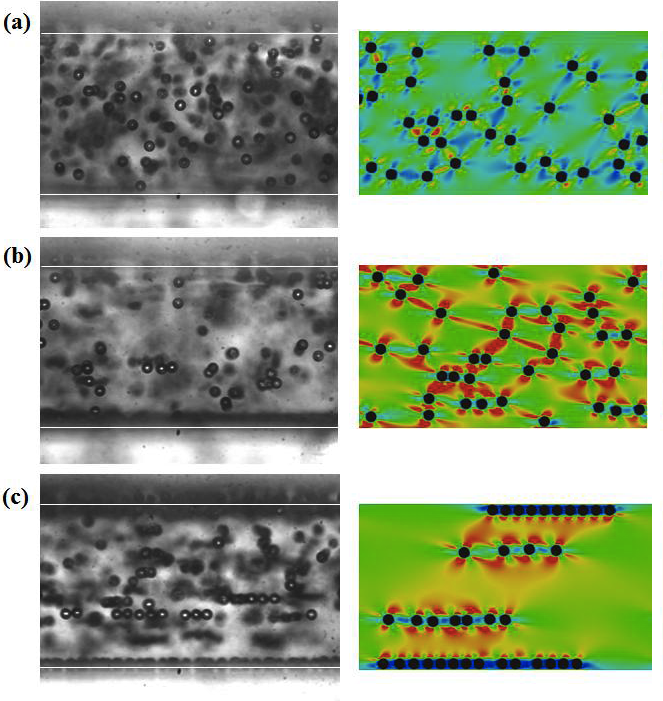
Fig. 1 – Snapshots of particle microstructure obtained by experiments (left) and simulations (right) taken at different times. The colors in the right panels represent the magnitude of the trace of the extra stress tensor.
It is well-known that particle chaining, i.e. the formation of strings of particles aligned along the flow direction, is a typical phenomenon related to the fluid viscoelasticity. In confined systems, particle migration can compete with the chaining phenomenon leading to different dynamics compared to those occurring in the bulk of the liquid far from the walls.
We carried out an experimental and numerical investigation on the chaining phenomenon in a confined shear flow aimed to clarify the role of migration on the formation of aligned structures [1]. A wormlike micellar solution is used as suspending liquid in the experiments that is modeled by the Giesekus constitutive equation in the simulations.
Experimental results show the formation of strings of particles in the bulk, along with the migration of a considerable amount of spheres towards the moving walls (see left panels of Fig. 1). At long times, chains in the bulk are stable, and cross-flow migration of individual spheres is suppressed.
Numerical simulations reproduce qualitatively the same phenomena observed experimentally, showing that a fast migration for those particles initially starting close the walls occurs, followed by a slower string formation (right panels of Fig. 1). An analysis of the trace of the extra stress tensor field (colors in the right panels of Fig. 1) allows to relate the formation of aligned particles to the existence of minima of the elastic energy in the fluid between the particles. Simulations with an Oldroyd-B constitutive equation with parameters chosen to reproduce the rheology of a Boger fluid do not show the presence of those minima. For such a fluid, indeed, no chaining is found and all the particles slowly migrate towards the walls, in agreement with previous experimental results.
Particle pairs and triplets in tube flow
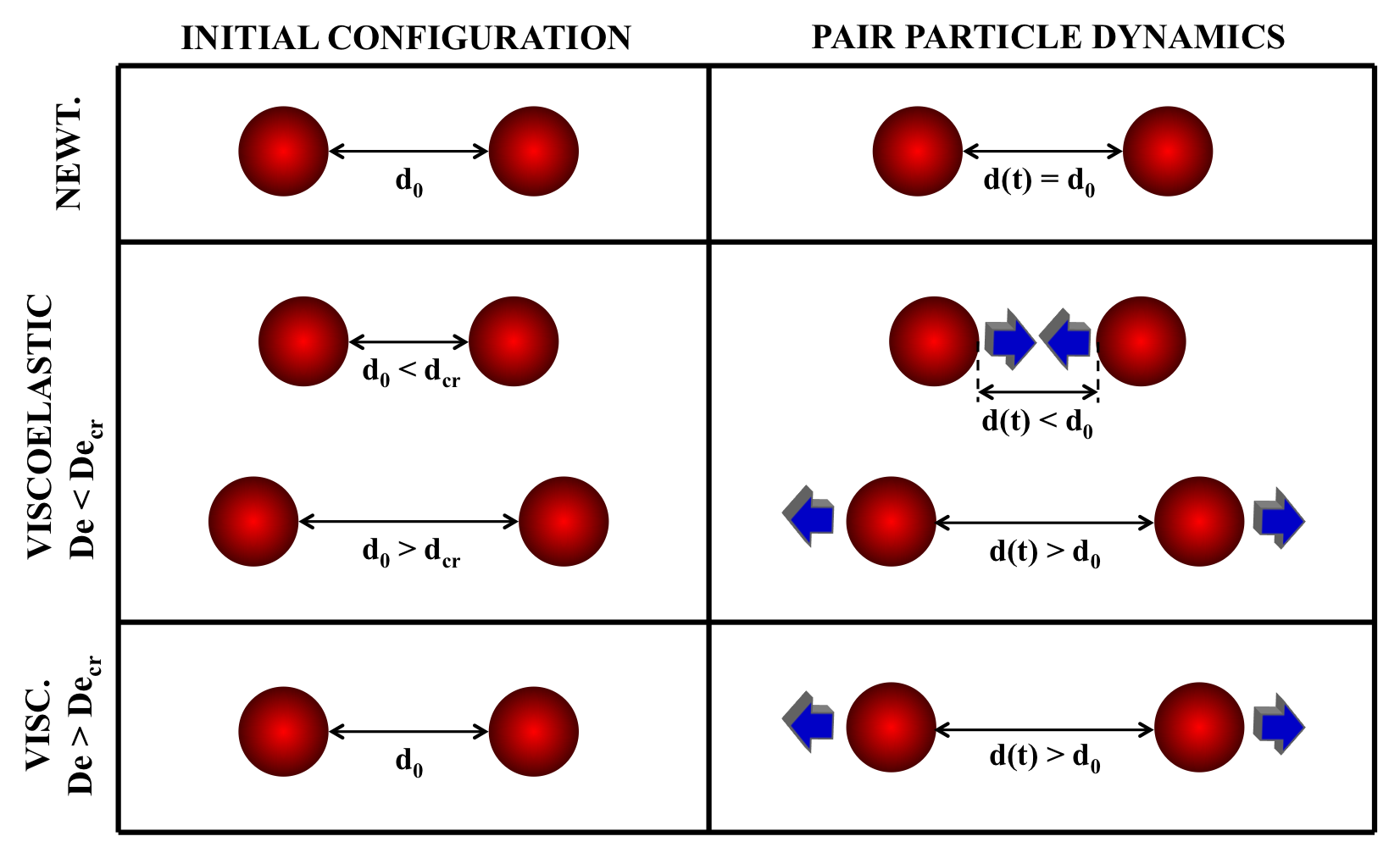
Fig. 1 – Pair particle dynamics for different suspending media. Left column: initial configuration with d0 the initial interparticle distance. Right column: pair particle dynamics with d(t) the time-dependent interparticle distance. Upper row: Newtonian case. Middle row: viscoelastic case with Deborah number lower than a critical value. Lower row: viscoelastic case with Deborah number higher than a critical value.
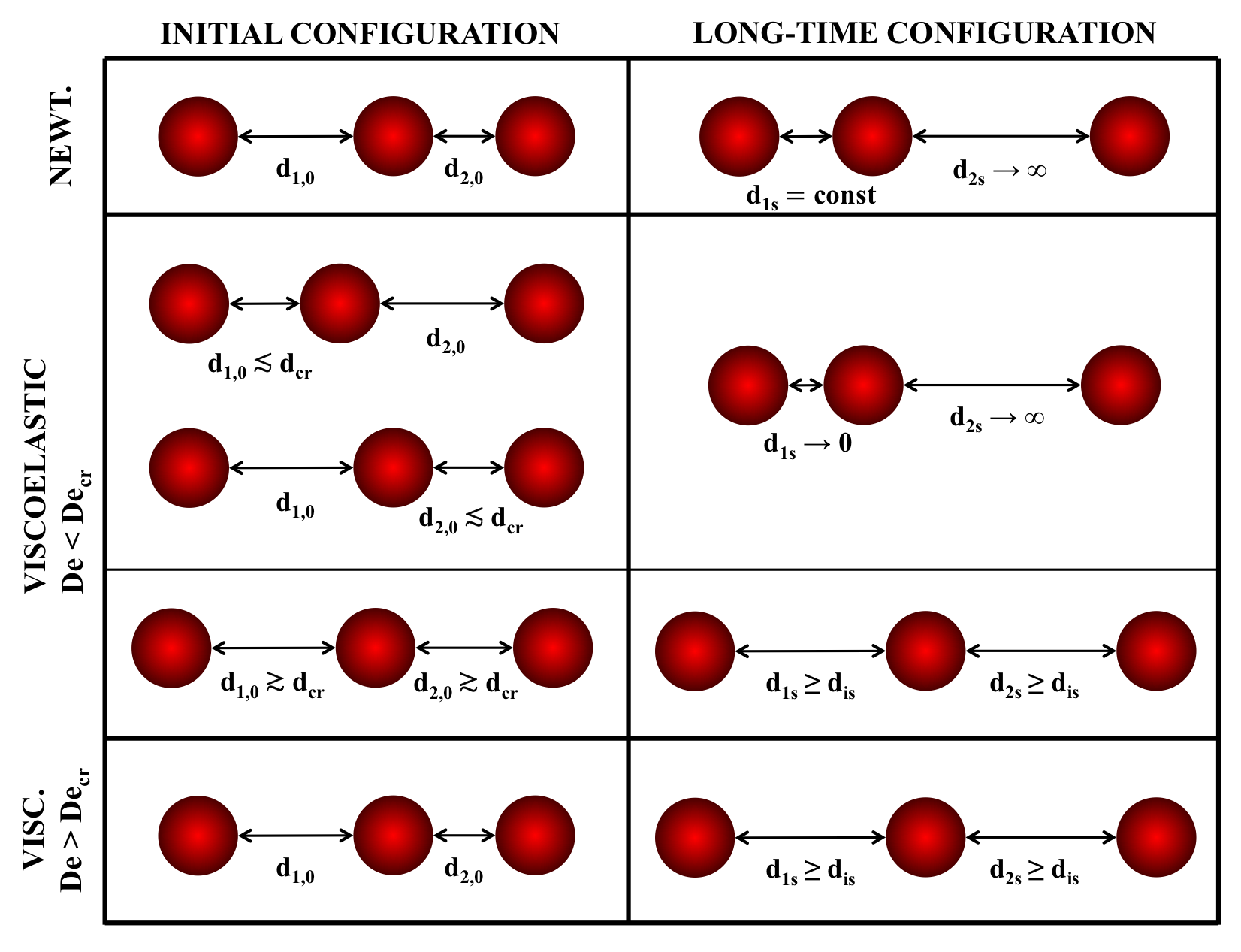
Fig. 2 -Three-particle dynamics for different suspending media. Left column: initial configuration with d1,0 the initial interparticle distance between the left and the middle particles, and d2,0 the initial interparticle distance between the middle and the right particles. Right column: long-time configuration with d1s and d2s the long-time interparticle distances. Upper row: Newtonian case. Middle rows: viscoelastic case with Deborah number lower than a critical value. Lower row: viscoelastic case with Deborah number higher than a critical value.
The dynamics of pairs and triplets of spherical particles flowing at the centerline of a cylindrical channel in a viscoelastic fluid is investigated [1,2]. For a pair of particles, at variance with the Newtonian case where the interparticle distance remains constant (upper panels of Fig. 1), the viscoelastic nature of the suspending medium alters the interparticle distance during the flow. For Deborah numbers lower than a critical value, the particles can approach or separate depending on the initial distance (central panels of Fig. 1). For Deborah numbers higher than such a critical value, the approaching dynamics disappears and the particles separate regardless of their initial distance (lower panels of Fig. 1).
The three-particle dynamics is more complex. In a Newtonian liquid, the leftmost particle of the triplet approaches and slows down the middle one. Consequently, the rightmost particle separates, giving rise to a pair and an isolated particle (upper panels of Fig. 2). For a viscoelastic liquid, different dynamics occur depending on the initial configuration and the Deborah number. For a Deborah number lower than the critical value found for the pair, if at least one of the initial distances between the left and the middle particles or the middle and the right particles is lower than the critical distance found for the pair, the long-time configuration is given by the left and the middle particles forming a pair with distance tending to zero, and the isolated right particle (upper row of the middle panels in Fig. 2). On the other hand, for both interparticle distances higher than the critical distance, the particles tend to separate until they do not hydrodynamically interact anymore (lower row of the middle panels in Fig. 2). Such a final configuration is also found for a Deborah number higher than the critical value, regardless of the initial distances (lower panels in Fig. 2).
- D’Avino et al., Comput. Fluids, 86, 45-55 (2013)
- D’Avino and Maffettone, Microfluidics and Nanofluidics, 23, 82 (2019)
Separation

Fig. 1 – Particle motion through a Deterministic Lateral Displacement device: velocity distribution (left) and finite element mesh (right)
Non-Newtonian fluids are more and more used for microfluidic applications as they allow to achieve operations such as focusing or separation in simpler devices as compared to Newtonian liquids. We demonstrated the possibility to tune the critical particle size in a Deterministic Lateral Displacement (DLD) separator by using shear-thinning fluids [1]. The DLD device consists in a sequence of rows of obstacles that are shifted by a fixed displacement along the flow direction (see Fig. 1). On the basis of their size, particles traveling through the array follow different paths and can be separated in outflow. Although very efficient in terms of speed and separation resolution, one limitation of such a technique is that each device works for a specific critical size to achieve particle separation, and a new device with different geometrical properties needs to be fabricated, as the dimensions of the particles to be separated change. Our simulations show that the viscosity thinning alters the flow field between two obstacles and, in turn, affects the critical particle radius. A real-time tuning of the characteristic separation size can be achieved by controlling the flow rate. A design formula relating the critical size to the geometrical parameters of the device and the fluid rheology is derived [1].
Rheology

Fig. 1 – Start-up dynamics of a viscoelastic suspension in planar elongational flow. The colors are the trace of the conformation tensor.
We studied the rheological properties of viscoelastic suspensions in planar elongational flow. To manage the exit of the particles from the computational domain, the latter is divided in three concentric regions [1-2]. If a particle crosses the boundary of the intermediate region, it is randomly relocated on one of the inflow section of the same region. The innermost domain is used to calculate the bulk properties of the suspension, the outermost is used to set the elongational flow boundary conditions far from the particles, and an intermediate region is used to allow the developing of viscoelastic stress fields around the particle after the relocation and before entering the innermost layer.
Local fields of the conformation tensor (see Fig. 1) show the existence of elongated elastic regions (red zones) where the polymer chains assume preferred orientations [2]. By integrating the local stresses, we get the bulk elongational viscosity that increases with both the solid fraction and the Weissenberg number. The strain hardening parameter is found to be a decreasing function of the solid fraction, confirming the experimental result that the strain hardening is suppressed by adding solid particles [2]. We explained such an effect by observing that, in concentrated systems, the hydrodynamic interactions lead to local shear flows between the particles that, in the case of shear-thinning fluids, contribute to reduce the suspension bulk viscosity [2].
- D’Avino et al., J. Comp. Phys., 226, 688-711 (2007)
- D’Avino et al., J. non-Newtonian Fluid Mech., 150, 65–79 (2008)
Numerical methods
We developed an efficient decoupled numerical scheme to solve the transient flow of viscoelastic fluids. Available decoupling schemes are based on two substeps: in the first substep the stress is computed at the new time level by using the velocity field at the previous step. In the next substep, the viscoelastic stress just calculated is used as known force term in the momentum balance. Although efficient and accurate, those schemes only work if inertia and/or a large Newtonian solvent contribution are included in the modeling. If this is not the case a singular matrix appears upon momentum balance discretization and no velocity update is possible. Instead of substituting the computed stress field in the momentum balance, we propose to use a time-discretized but space-continuous form of the constitutive equation based on a first-order, semi-implicit Euler scheme [1]. This adds velocity unknowns in the momentum equation even if the solvent viscosity is zero, thus allowing the computation of the velocity field. In the second substep, a second-order semi-implicit Gear-based scheme is used to update the stress tensor at the new time level. This method has been proven to be second-order accurate. More recently, the proposed stress-implicit scheme has been extended to account for inertial terms, showing stability and accuracy improvements over traditional decoupled algorithms [2].