Manager: Massimiliano M. Villone (http://dicdot16.ingchim.unina.it/wordpress/?page_id=346)
Members:
Marco Trofa (http://dicdot16.ingchim.unina.it/wordpress/?page_id=634)
Expertise: Computational Fluid Dynamics (CFD), computational rheology, soft matter, deformable interfaces, suspensions, emulsions, foams
Tools: Finite Element Method (FEM) Direct Numerical Simulations (DNS)
In several fields of scientific and technological interest, e.g., blood circulation, microfluidics, polymer processing, …, it is likely to `meet’ multiphase systems in which a suspending liquid contains inclusions whose shape can change due to applied physical stimuli. Some examples are suspensions of soft solid beads (like gel microparticles) and cells, emulsions (i.e., liquid droplets dispersed in an immiscible liquid matrix), foams (gas bubbles dispersed in a liquid matrix).
The `core business’ of the Officina is the direct numerical simulation of the behaviour of suspensions with deformable inclusions of different types and shapes under many flow conditions.
Since the rigorous presentation of the quantitative results and the technical details concerning the numerical techniques can be found in the scientific papers (http://dicdot16.ingchim.unina.it/wordpress/?page_id=142), this Section is devoted to CFD in the sense of Cartoon Fluid Dynamics. In other words, videos of the dynamics of several kinds of suspensions with deformable inclusions (yet, obtained through the actual numerical simulation results) are shown in order to give the most immediate description of the behaviour of such systems.
Deformation and lateral migration of elastic particles
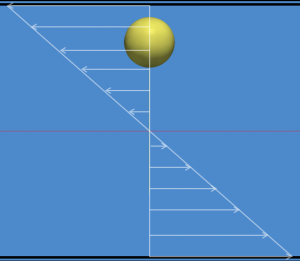
When an initially spherical elastic particle is suspended in a liquid subjected to unbounded shear flow, the hydrodynamic forces exterted by the liquid makes the particle deform until attaining an steady-state ellipsoidal shape (click to see video).
When an initially spherical elastic particle is suspended in a liquid subjected to confined shear/tube flow, the hydrodynamic forces exterted by the liquid and the interactions with the flow cell walls make the particle deform into asymmetric shapes. In addition, another phenomenon superimposes to deformation, namely, particle lateral migration orthogonally to the suspending liquid streaminlines towards the flow cell symmetry plane/axis (click to see videos of particle lateral migration in confined shear and tube flow).
When an elastic particle of non-spherical shape at rest, e.g., a prolate spheroidal particle, is suspended in a liquid subjected to confined shear flow, it undergoes lateral migration with shape oscillations (click to see video).
Detailed quantitative investigations on the effects of the geometrical and physical parameters on the above mentioned phenomena can be found in the following papers:
- M. M. Villone, M. A. Hulsen, P. D. Anderson and P. L. Maffettone, Simulations of deformable systems in fluids under shear flow using an arbitrary Lagrangian Eulerian technique, Computers and Fluids, 90, 88-100 (2014)
- M. M. Villone, F. Greco, M. A. Hulsen and P. L. Maffettone, Simulations of an elastic particle in Newtonian and viscoelastic fluids subjected to confined shear flow, Journal of Non-Newtonian Fluid Mechanics, 110, 47-55 (2014)
- M. M. Villone, G. D’Avino, M. A. Hulsen and P. L. Maffettone, Dynamics of prolate spheroidal elastic particles in confined shear flow, Physical Review E, 92, 062303 (2015)
- M. M. Villone, F. Greco, M. A. Hulsen and P. L. Maffettone, Numerical simulations of deformable particle lateral migration in tube flow of Newtonian and viscoelastic media, Journal of Non-Newtonian Fluid Mechanics, 234, 105-113 (2016)
Deformability-based separation of elastic particles
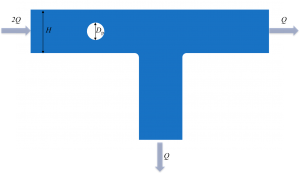
If a sample of deformable beads with different elastic properties is suspended in a Newtonian liquid flowing through a straight microfludic channel, a T-shaped bifurcation can be employed to separate particles depending on their deformability. Indeed, in the proximity of the bifurcation corner, stiffer beads will go straight, whereas softer ones will be deviated to the side outlet branch (click to see the what a soft particle does).
A quantitative investigation of separation conditions at varying the constitutive and operating parameters can be found in
- M. Trofa, M. M. Villone, G. D’Avino, M. A. Hulsen, P. A. Netti and P. L. Maffettone, Numerical simulations of the separation of elastic particles in a T-shaped bifurcation, Journal of Non-Newtonian Fluid Mechanics, 233, 75-84 (2016)
In silico measurements of the linear viscoelastic properties of emulsions
Every emulsion, even if consisting in a suspension of Newtonian liquid droplets in a Newtonian matrix, shows viscoelastic properties. It is possible to get a measure of the storage and loss moduli G’ and G” of the system by measuring the shear stress in its bulk while it undergoes Small Amplitude Oscillatory Shear (SAOS) flow (click to see video).
Quantitative in silico measurements of the viscoelastic properties of emulsions of Newtonian drops in a Newtonian matrix at varying the constitutive and operating parameters, with the validation of a literature theoretical model, are reported in
- M. M. Villone, G. D’Avino, M. A. Hulsen, F. Greco and P. L. Maffettone, Numerical simulations of linear viscoelasticity of monodisperse emulsions of Newtonian drops in a Newtonian fluid from dilute to concentrated regime, Rheologica Acta, 53, 401-416 (2014)
Viscoelastic liquid foaming and film retraction
In a foam, the liquid between two (or more) growing gas bubbles gets squeezed until becoming a thin film, which can rupture when it reaches a critical thickness or due to the presence of impurities. After the hole has formed, it broadens to an extent depending on the interplay among surface, inertial, viscous, and, eventually, elastic forces (if the liquid is viscoelastic), thus making the film between the two bubbles retract. This has an important effect on the morphology of the resulting system (click to the video of bubble growth).