The Officina Microfluidics aims to develop devices able to perform unitary operations such as focusing, separation, spacing by exploiting non-linear rheological properties of complex fluids. This Officina is strictly connected to the Officina Viscoelastic Fluid Dynamics providing the required theoretical understanding to design efficient microfluidic devices.
Manager: Gaetano D’Avino, Daniele Tammaro, Massimiliano Villone
Members: Lorenzo Lombardi
Viscoelastic Focusing of Spherical MicroParticles

Fig. 1 – Distributions of particles suspended in a PVP solution flowing in a cylindrical microchannel. Snapshots taken at 2.5 cm (a), 3.5 cm (b) and 4.5 cm (c) from the channel inlet are reported
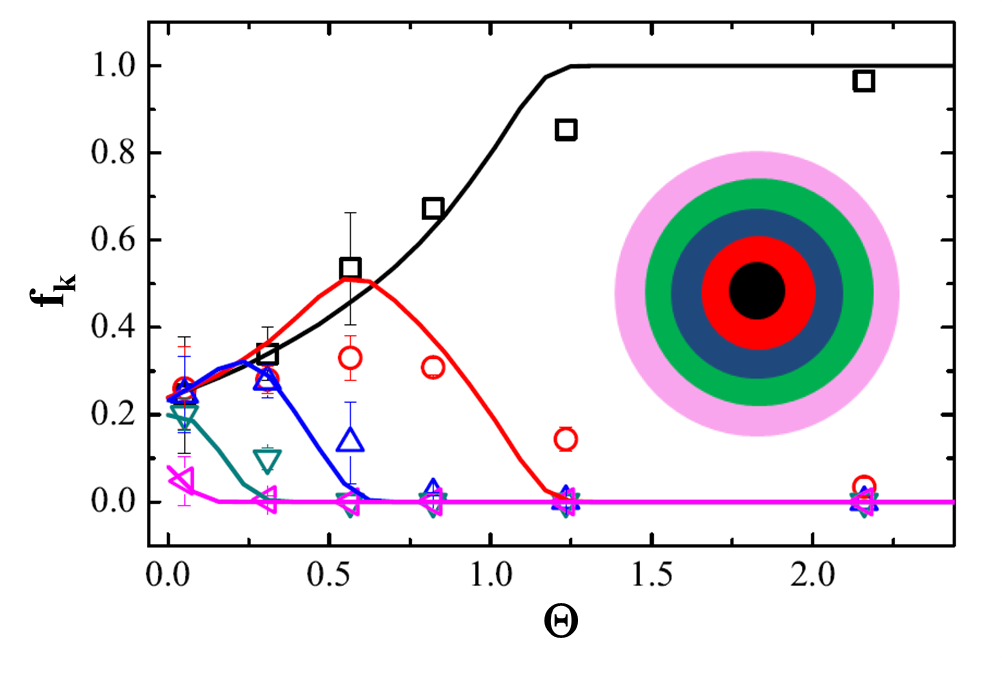
Fig. 2 – Measured (symbols) and computed (lines) fractions of particles in the band k as a function of the dimensionless parameter Θ. The inset shows schematically how the channel cross-section is divided in annular bands
The 3D flow-focusing, i.e. the ability to generate files of particles along a streamline of the flow field, is required in several microfluidic applications such as detection, counting, separation. We demonstrated that 3D focusing can be obtained through viscoelasticity-induced migration of noncolloidal spheres in pressure-driven flows in simple cylindrical channels in a wide range of flow rates. Numerical simulations (see “Particle migration” in Officina Viscoelastic Fluid Dynamics) suggest the optimal fluid rheology allowing to maximize the efficiency of the focusing [1]. Experiments performed with 4 μm polystyrene particles suspended in a acqueous solution of polyvinylpyrolidone (PVP) flowing in a 50 μm micropipe confirm the single-line focusing (Fig. 1).
The fraction of particles measured at different distances from the inlet and flow rates is in good quantitative agreement with the computed ones (Fig. 2). By generalizing previous asymptotic analytical theories through numerical simulations, we show that the focusing mechanism is governed by a single dimensionless number θ that accounts for all the relevant fluid, flow and geometrical quantities [2]. The experimental particle distributions along the channel axial direction collapse on a single curve when rescaled in terms of the proposed dimensionless number (Fig. 3). A simple formula to design a viscoelasticity flow-focusing device is derived [1, 2].
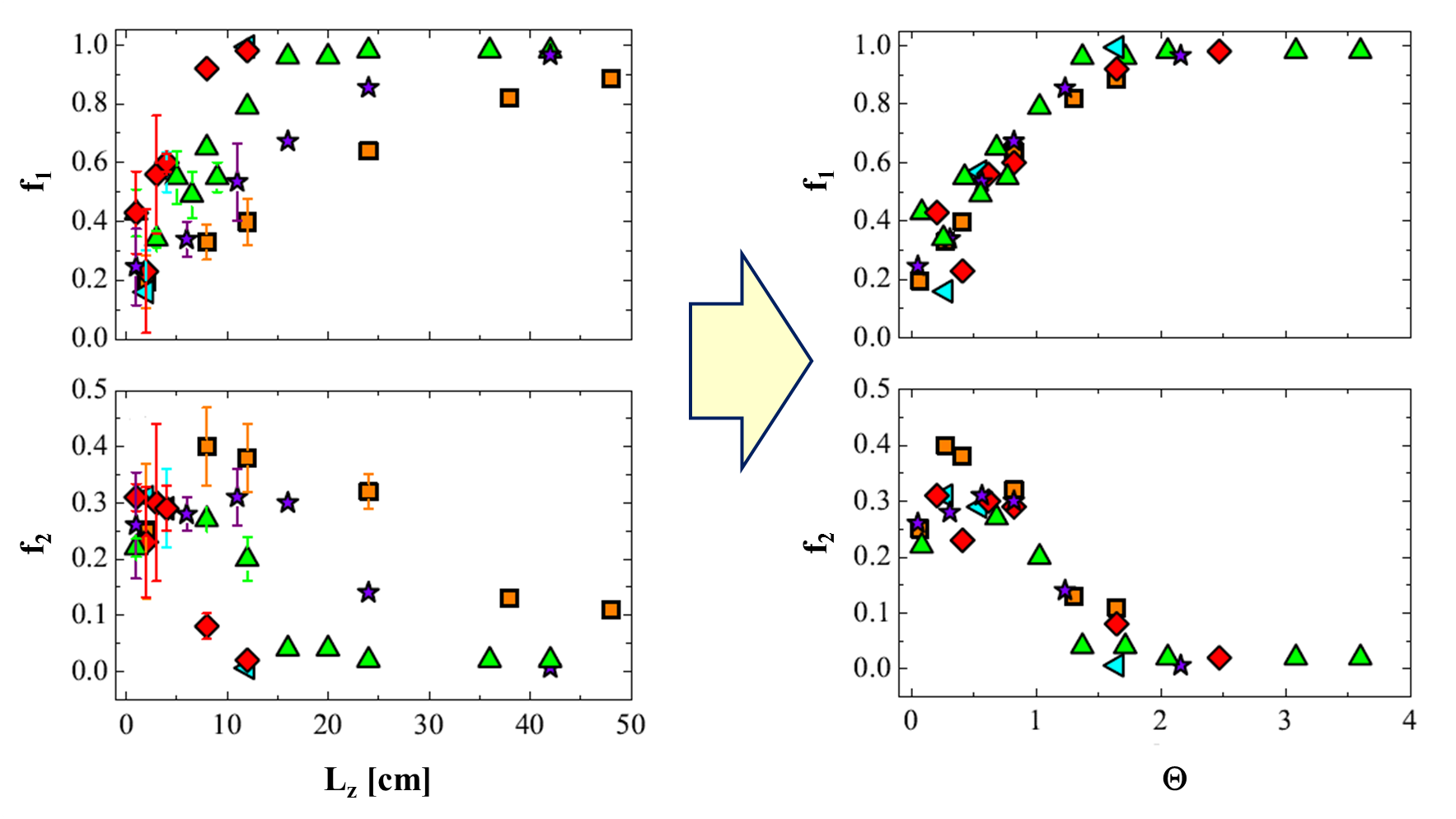
Fig. 3 – Left panels: experimentally measured particle fraction in the first band (top) and in the second band (bottom) as a function of the distance from the inlet for different flow rates. Right panels: experimentally measured particle fraction in the first band (top) and in the second band (bottom) rescaled according to the dimensionless parameter Θ.
Those results have been extended to square-shaped microchannels [3]. We made experiments to study the migration of spherical rigid particles with diameter of 6 μm, suspended in the acqueus solution of PVP, in a channel with the side of cross section of 50 μm. Particle alignment along the channel centerline is found in such a geometry as well (see Fig. 4a). Higher Deborah numbers promote particle focusing. A method to reconstruct particle positions in the channel cross-section by coupling particle tracking analysis and numerical simulations is proposed [3] (see Fig. 4b e 4c).
The measured particle fractions can be rescaled according to a single dimensionless parameter, as already reported for the case of cylindrical channels. The so-obtained master curve can be used as a guide to predict the required focusing length.
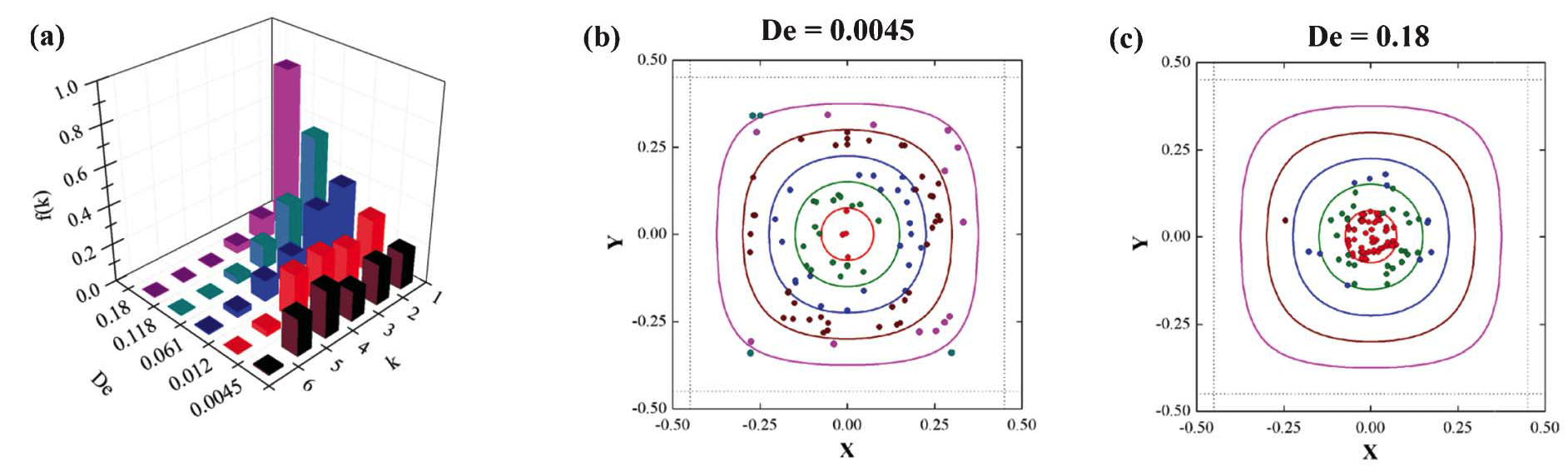
Fig. 4 – Experimental results for the 50 micron channel. (a) Fractions of particles in the different k bands measured at 4 cm from the inlet as a function of the Deborah number. (b) Particle positions on the square cross-section at De = 0.0045. The symbols denote the position of the particle centers and are colored according the band they belong to. (c) Particle positions as in (b), at De = 0.18.
1. D’Avino et al., Lab Chip, 12, 1638-1645 (2012)
2. Romeo et al., Lab Chip, 13, 2802-2807 (2013)
3. Del Giudice et al., Lab Chip, 13, 4263-4271 (2013)
Viscoelastic Focusing of NanoParticles
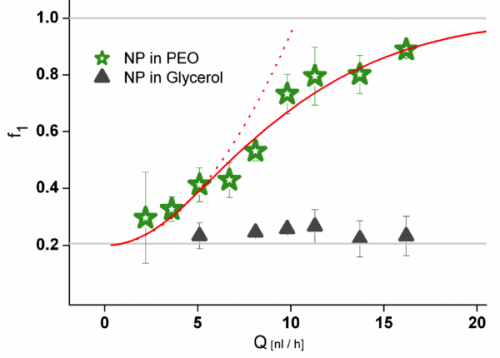
Fig. 5 – Particle fraction in the innermost band of a microtube for different flow rates for a 0.3 wt % PEO aqueous solution (green stars) and for a 55 wt % glycerol in ionized water (black triangles). The red line is a theoretical predictions and the dashed line is the limit of the prediction at low flow rates.
Fluid viscoelasticity can be exploited to trap nanoscopic objects around the centerline of a micro tube as well [1]. When dealing with nanoparticles, thermal motion becomes important, and the diffusive effects of Brownian forces act on the flowing nanoparticles. Such diffusion works against fluid elasticity that, if alone, would force the particles to flow trapped at specific streamlines as discussed above for micrometric objects. We demonstrated, however, that the Brownian motion in a suspension of nanoparticles can be counteracted, in flow, by the viscoelastic properties of a suspending liquid. The trapping efficiency depends on the squared flow rate. Figure 5 shows the fraction of particles (radius of 100 nm) migrated in a region of radius 500 nm around the centerline of a tube with radius 2.5 microns. Two suspending fluids are considered: a 0.3 wt % PEO aqueous solution (green stars) and a 55 wt % glycerol in deionized water (black triangles). The data are taken at different flow rates and at a distance of 6 cm from the channel inlet. All the measurements are at equilibrium, i.e. the same fraction is found at 4 cm and 8 cm from the inlet. It is readily shown that while no focusing is observed in the Newtonian fluid, alignment is found at high flow rates in the viscoelastic liquid. It is worthwhile to point out that a qualitative different scenario occurs for microparticles, i.e. when diffusion is negligible. Indeed, in this latter case, a sufficiently large distance from the inlet by which all particles are trapped along the centerline always exists. Conversely, when Brownian motion becomes relevant, diffusion prohibits trapping, whatever is the distance from the inlet: a certain variance of the steady-state particle distribution is always present. This is what happens at low flow rates in Fig. 5 where the fraction of particles at equilibrium around the centerline cannot reach unity values.
The solid red curve in Fig. 5 comes from a theoretical prediction obtained by balancing drag, elastic and Brownian forces acting on the particle [1]. Finally, the dashed red curve is the limit at low flow rates of the solid red curve which highlight a quadratic dependence of the trapping capability with the flow rate.
1. De Santo et al., Phys. Rev. Applied, 2, 064001 (2014)
Viscoelastic Ordering
Fluid viscoelasticity can be exploited to generate a microstructure of equally-spaced particles along the centerline of a straight microfluidic channel, referred as particle ordering. Experiments show that particles with diameter d = 20 μm first align at the channel centerline of a square-shaped glass microchannel with height H = 100 μm and then self-order, forming trains with a throughput up to 2400 particles/s [1] (see Fig. 6).
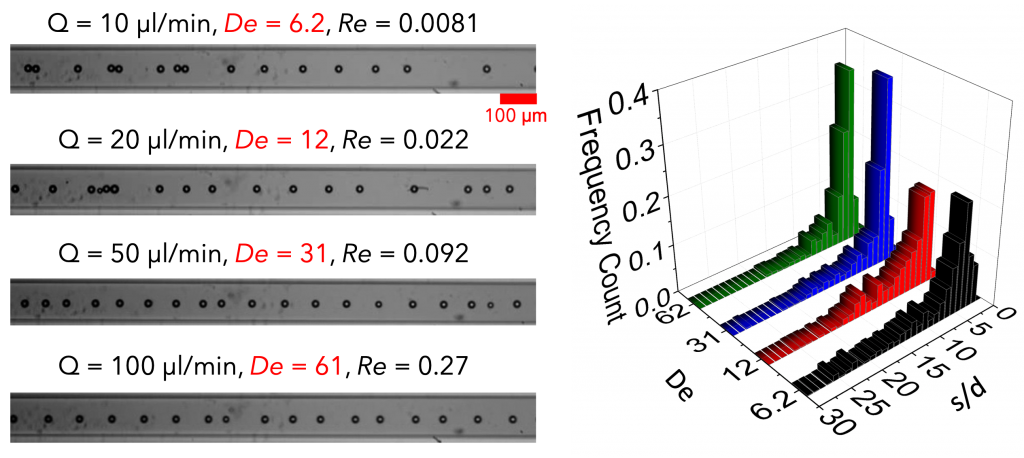
Fig. 6 – (Left) Particle microstructure for spherical particles with a diameter of 10 microns in a square-shaped straight microchannel with side 100 microns at different flow rates. The corresponding Deborah and Reynolds numbers are reported. (Right) Distributions of the interparticle distances for different Deborah numbers.
Particle trains in viscoelastic liquids are thus easily formed, without the need to design complex microfluidic platforms or to use external control systems. Shear-thinning of the suspending liquid is required to achieve the ordering. Numerical simulations confirm the experimental findings [1,2], highlighting that the spatial evolution of the microstructure strongly depends on the particle linear concentration and the initial distance distribution. In general, at very low volume fractions, weak hydrodynamic interactions prevent significant changes of the initial microstructure. At intermediate values of the particle concentration, ordering is possible. At high volume fractions, strings of nearly-touching particles form. A partially ordered structure in inflow strongly increases the ordering efficiency. Experimental and numerical evidence can be justified by a simple stability analysis, based on the presence of an effective peculiar repulsive potential between particles. In channel flows, this repulsive field, which stems from hydrodynamic interactions in viscoelastic liquids at large Deborah numbers, promotes either particle ordering or particle pairing. From the same stability argument, it comes out that particle pairing, which is detrimental in applications related to flow cytometry and encapsulation, can be avoided by tuning the fluid rheology and particle concentration. The effect of confinement ratio [3] and surface properties of the microchannel walls [4] on particle ordering are also investigated.
1. Del Giudice et al., Phys. Rev. Applied, 10, 064058 (2016)
2. D’Avino and Maffettone, Meccanica, 55, 317-330 (2020)
3. Jeyasountharan et al., Phys. Fluids, 34, 042015 (2022)
4. D’Avino and Maffettone, Electrophoresis, 43, 2206-2216 (2022)
